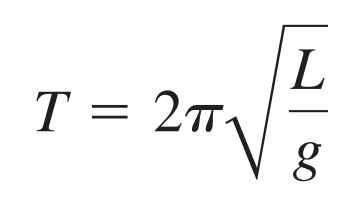A GUT (grand unified theory) refers to theories that ...

Question

A GUT (grand unified theory) refers to theories that 

Answer

A) unify all four forces. 

B) unify gravity and the electromagnetic and weak forces. 

C) unify gravity and the strong and weak forces. 

* D) unify the strong force and the electromagnetic and weak forces. 

E) unify the electromagnetic and weak forces.

Period of small-angle oscillations of a simple pendulum

 

Lab 3 Acceleration due to Gravity Using a Simple Pendulum

 

	Borough of Manhattan Community College
	The City University of New York
	SCIENCE DEPARTMENT
	Laboratory Experiment
	Lab 3: ACCELERATION DUE TO GRAVITY
	USING A SIMPLE PENDULUM
Student Last Name			First Name
Accepted g=	9.8	m/s²
		Measured and Calculated Data
Pendulum Length L (m)	Time t for 15 swings (s)	Period T (s) T=t/15	Period Squared T² (s²)	g =4𝛑²L/T² (m/s²)	%Error
1	2	3	4	5	6
	Measured Data	B13/15	C13^2	4*pi()^2*A13/D13	abs(g-E13)/g*100
0.30
0.55
0.75
1.00
			g average (m/s²) =		average(E13:E16)
			% Error =		abs(g-E17)/g*100
	Table of Prepared Data for Plotting the Scatter Chart
	Pendulum Length L (m)	Period Squared T² (s²)
Slope (s²/m)		slope(C21:C24,B21:B24)
g = 4𝛑²/Slope (m/s²)		4*pi()^2/B26
% Error		abs(9.8-B27)/9.8*100
Conclusion:
Plot

🧲 Slope of the Plot of y versus x

If the relationship between the physical parameters y and x in some physical process is described by the equation

 y = a x + b, 

then the theoretical slope of the plot of y versus x is equal to a.

Rotational inertia

 

What is Average Power Output?

 

What is the maximum compression of the spring?

A mass m₁=[m] kg is at rest on a frictionless horizontal surface and connected to a wall by an ideal spring with a spring constant k = [k] N/m as shown in the figure. 

 A second mass m₂ =[mm] kg is moving to the left at speed v₀=[v] m/s. 

The two masses then collide elastically. 

 What is the maximum compression of the spring? 

Give your answer in m using 3 significant figures.

Root-mean-square Distance

The average distance x_rms that a molecule travels  by diffusion is proportional to the square root of time:

x_rms = √ (2Dt)

where
x_rms stands for the root-mean-square distance and is the statistical average for the process,
D is the diffusion constant for the particular molecule in a specific medium. 

t = x_rms² /  (2D)

t₁ = x_1rms² /  (2D)

t₂ = x_2rms² /  (2D)

t₂  /  t₁ = x_2rms²  /   x_1rms²

t₂ = t₁ x_2rms²  /   x_1rms²

Bernoulli’s Equation

Bernoulli’s equation states that for an incompressible, frictionless fluid, the following sum is constant:

P + ½ ρ v² + ρ g h = constant,

where
P is the absolute pressure,
ρ is the fluid density,
v is the velocity of the fluid,
h is the height above some reference point, and
g is the acceleration due to gravity.

Velocity Measurement

Figure shows two devices that measure fluid velocity based on Bernoulli’s principle. 

The manometer in Figure (a) is connected to two tubes that are small enough not to appreciably disturb the flow. The tube facing the oncoming fluid creates a dead spot having zero velocity ( v₁=0 ) in front of it, while fluid passing the other tube has velocity v₂. 

 This means that Bernoulli’s principle as stated in 

 P₁ + ¹/₂ ρv₁² = P₂ + ¹/₂ ρv₂² 

 becomes 

 P₁ = P₂ + ¹/₂ ρv₂². 

 Part a of the figure shows a picture of a wing. It is in the form of an aerofoil. One side of the wing is broader and the other end tapers. The direction of the air is shown as lines along the length of the wing. The direction of the air below the wing is shown as flowing along the length of the wing. The pressure exerted by the air given by P b is upward. The direction of the air on the top or front part of the wing is shown as flowing along the length of the wing. The pressure exerted by the air is given by P f, and it acts downward. Part b of the figure shows a boat with a sail. The direction of the sail is almost across the boat. The direction of the air in the sail is shown by lines on the front and back sides of the sail. The air currents on the front exert a pressure P front toward the sail, and air currents on the back sides of sail exert a pressure P back again toward the sail. Thus pressure P₂ over the second opening is reduced by ¹/₂ ρv₂² , and so the fluid in the manometer rises by h on the side connected to the second opening, where 

 h ∝ ¹/₂ ρv₂² 

(Recall that the symbol ∝ means “proportional to.”) 

Solving for v₂ , we see that 

 v₂ ∝ √h 

 Figure (b) shows a version of this device that is in common use for measuring various fluid velocities; such devices are frequently used as air speed indicators in aircraft.

⁰ ¹ ² ³ ⁴ ⁵ ⁶ ⁷ ⁸ ⁹ ⁺ ⁻ ⁼ ⁽ ⁾ ⁿ ⁱ₀ ₁ ₂ ₃ ₄ ₅ ₆ ₇ ₈ ₉ ₊ ₋ ₌ ₍ ₎ ₐ ₑ ₒ ₓ ₔ ₕ ₖ ₗ ₘ ₙ ₚ ₛ ₜ .

Flow rate Q

Flow rate Q is defined to be the volume of fluid passing by some location through an area during a period of time, as seen in Figure.  

In symbols, this can be written as 

Q = V / t,  

where 

V is the volume and

t is the elapsed time. 

The SI unit for flow rate is m³/s, but a number of other units for Q are in common use. 

 For example, the heart of a resting adult pumps blood at a rate of 5.00 liters per minute (L/min).  

Note that a liter (L) is 1/1000 of a cubic meter or 1000 cubic centimeters ( 10⁻³m³ or 10³cm³ ).

The precise relationship between flow rate Q and velocity v is

Q = A v,

where
A is the cross-sectional area and
v is the average velocity.

Rod half-and-half